Powell Says Fed Is Ready to Raise Rates Faster If Needed The CME FedWatch tool is based on current fed fund futures quotes around the FOMC meetings and the assumption of gradual fed fund rate changes (+/- 0.25%). In the list below, more than 50% probability is used to indicate rate hike; “+” is shown after the FOMC date to indicate that rate hike can be at that or a later FOMC.
2nd & 3rd rate hike, FOMC 5/4/22+ (so, possible 50-bps hike)
4th & 5th rate hikes, FOMC 6/
15/22+ (so, possible 50-bps hike)
6th rate hike, FOMC 7/27/22+
7th rate hike, FOMC 9/2
1/22+
8th rate hike, FOMC
11/2/22+
9th rate hike, FOMC
12/
14/22+
Powell's tough talk moved the rate hike expectations a LOT. Some say that the strategy may be to talk very tough, move the fed fund futures markets and then may be do less than what is in the market.
https://www.cmegroup.com/trading/interest-rates/countdown-to-fomc.html
Morningstar Portf. Manager speed That's one hell of a fast connection. Mine here in SF is only about 10 and 2, and that's plenty fast enough for everything that I'm doing, including watching two Amazon Prime downloads simultaneously (though on relatively small screens).
Morningstar Portf. Manager speed Download: 123.7. Upload 17.7
U.S. inflation rate climbs again to 7.9%, CPI shows / MarketWatch Article
Buy Sell Why: ad infinitum. Funnyman WB. He is paying $848.02 for his newest acquisition Alleghany/
Y. Why such an odd price? Well, that is $850 minus the fee for Goldman Sachs/
GS that Y is paying - WB doesn't think GS found him as buyer for Y and his cash offer doesn't need any fancy footwork from GS.
Alleghany/Y was captured in my summary then (although I didn't buy it)
LINK"BULLISH. Insurer Alleghany (Y; no dividends but special dividends with the last one in 2020; fwd P/E
14.
1 (202
1), 9.7 (2022); P/B
1; like mini-BRK; businesses include P&C insurance, reinsurance and noninsurance businesses such as steel fabrication, toys, funeral products, etc; pg
15);"
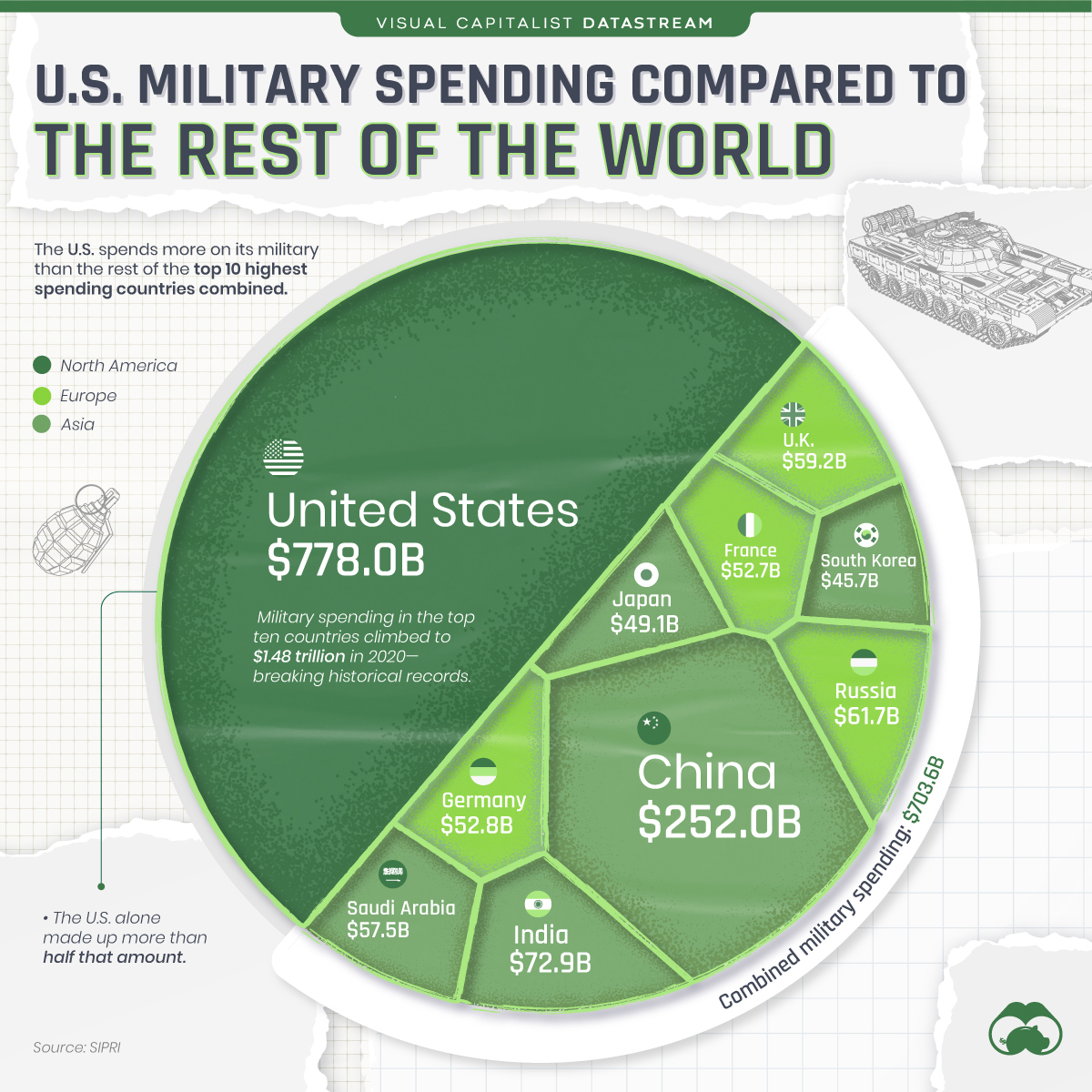
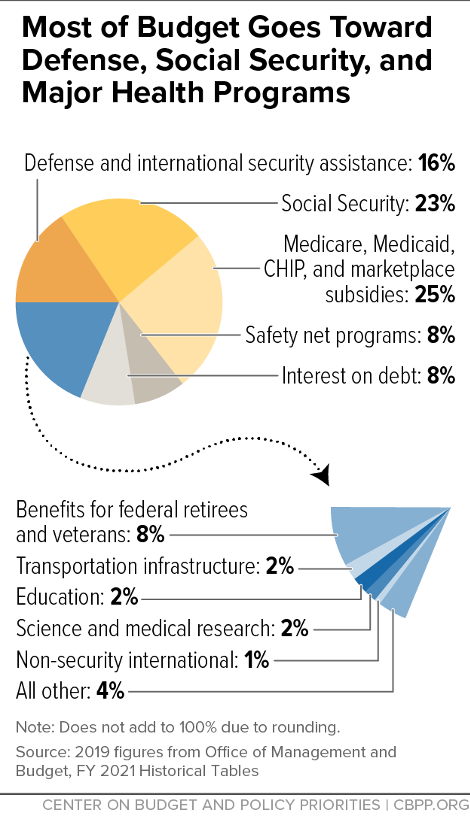
2022’s Most & Least Federally Dependent States +1
Tough Day in Bond Land Part of the curve is inverted. The 5 year Treasury is yielding more than the 10 year. Just noticed this evening. Probably been evident for a while.
I don’t know of any sure fire remedies for investors. I’m pretty much staying the course. But did trim fixed income exposure from 30 to 25% within past month. Of course, many of my alternative & allocation funds also hold fixed income - so the real % is higher. I’m eager to see if D&C can turn the losses in DODIX around before year end. This is not a fund that’s accustomed to negative returns. Let’s not forget some of these funds pay interest quarterly and that will lessen some of the hit.
CVSIX is off 1.63% YTD. That’s probably the “best” performer of any of my fixed invome funds this year.
My most interesting “bond” fund is GLDB. Off 3% YTD. Chart resembles a pogo-stick as it’s very erratic. New fund. Only $3 M AUM. They appear to hold longer dated corporates / investment grade bonds and somehow back them with gold bullion. The idea is that if the dollar slides in value the bonds will hold their value better. The effect seems to be that on any given day you get about 2/3 the movement in gold’s price and about 1/3 the movement in 10-15 year corporate bonds. It kicks out a little interest every month. Today the fund was up 1% pretty much in line with gold mining stocks. My hold on this fund is small - only about 2-3% of portfolio. BTW: I don’t count this one as fixed income - too weird. It is part of my 10% spec position which is designed to hedge against steep equity losses.
Buy Sell Why: ad infinitum. WB understands insurance business well since Berkshire Hathaway owns several insurance companies including Geico. It is challenging for someone to overcome this acquisition with over $11B in cash.
I too read Barron’s but often fail to follow up on the stories as you did. Again, job well done.
Buy Sell Why: ad infinitum. “there’s what 25 days to see if Allegheny receives a better offer? You could always throw that 5% in a high flier like BRK.B ?”Ummm … Good point. I’m not familiar with the legalities here. Is Berkshire locked in to the offer for 25 days? I’d have to guess that’s a very generous offer. Will be surprised if anyone tops it. FWIW: I sold at $846 having put in a limit offer before open. Y closed at $844.60. So there was a slight drift down during the day.
Rocked my boat seeing it up 25% in the pre market hours. I’m very old and very conservative. Would have settled for 25% over 2 or 3 years. Already have 2 stocks in the growth sleeve. Having this one in the more conservative “alternative” sleeve was a real reach in the first place.
Below is a link to the
Barron’s article that whetted my appetite last November. I tracked and studied the company for over 3 months before deciding to take a bite. Averaged in during February / March while it was falling. Bottomed at $588 March 8. Currently $844.60
https://www.barrons.com/articles/buy-alleghany-stock-berkshire-hathaway-pick-51636151493But thanks for the thoughts.
BTW - I think
Barron’s is underappreciated.
Tough Day in Bond Land Many core bond funds are down 4-5%. Short duration bonds loss less. Nevertheless, the 2.5 month loss is much less than those of stock fund loss in a single day. We put some $ into I bond since last year. Unfortunately, it is limited to $10K per person, plus $5k from your tax refund (assuming you get a refund that year).
Harbor Strategic Growth Fund is to be reorganized
Tough Day in Bond Land @larryB. +
1. Gotta do some serious thinking and choosing. Not much of my stuff is free and clear, outside of a tax-sheltered firewall. The lion's share is in T-IRA.
Harbor Strategic Growth Fund is to be reorganized @yogibearbull, What is Harbor trying to accomplish? Just selling AUM? Admin shares could have been converted without going through an asset transfer Reorganization.
If the acquiring fund does not retain the NAV price of the acquired fund on the date of the Reorganization (i.e., stock split), a shareholder could be disadvantaged because OEFs are only required to price in two decimals. For example, a shareholder's daily experience of the NAV changes of a $30 NAV fund is not the same as three shares at $
10 each of the same fund. The lower NAV gives a lumpy (non-continuous) price experience. I paid attention to this only after I bought a fund with a NAV in the $5 range.
2022’s Most & Least Federally Dependent States The fraud in the Covid relief is shameful, but it is misguided to assume that some billions fraudulently misappropriated in $5.
1 trillion worth of two relief--2020 and 202
1--packages indicate some sort of failure in policy:
https://cbpp.org/research/poverty-and-inequality/robust-covid-relief-achieved-historic-gains-against-poverty-and
When COVID-19 began to rapidly spread across the United States in March 2020, the economy quickly shed more than 20 million jobs. Amid intense fear and hardship, federal policymakers responded, enacting five relief bills in 2020 that provided an estimated $3.3 trillion of relief and the American Rescue Plan in 2021, which added another $1.8 trillion. This robust policy response helped make the COVID-19 recession the shortest on record and helped fuel an economic recovery that has brought the unemployment rate, which peaked at 14.8 percent in April 2020, down to 4.0 percent. One measure of annual poverty declined by the most on record in 2020, in data back to 1967, and the number of uninsured people remained stable, rather than rising as typically happens with large-scale job loss. Various data indicate that in 2021, relief measures reduced poverty, helped people access health coverage, and reduced hardships like inability to afford food or meet other basic needs.
These positive results contrast with the Great Recession of 2007-2009, when the federal response was large compared to measures taken in other post-World War II recessions but less than one-third as large as the fiscal policy measures adopted in 2020-2021, when measured as a share of the economy. While decried by some at the time as too large, the relief measures enacted during the Great Recession were undersized and ended too soon. As a result, the economy remained weak for longer than was necessary — and families suffered avoidable hardship. Two years after the Great Recession began, unemployment was still 9.9 percent and food insecurity remained one-third above its pre-recession level. While some of that difference stems from differences in the trigger to the downturn, some is clearly due to the strength of the policy response.
What I don't like is states and politicians claiming they don't need federal assistance and shouldn't have to pay taxes while taking loads of federal assistance.